Class dedicated to degeneration processing when looking for neighbours.
Let A be a polytope of \( \mathbb{R}^n, A = H_1^+ \cap H_2^+ \cap ... H_{n-1}^+ \cap ... H_k^+ \) where k>n.
Let [vi, vj] be a segment of two vertices of A such as:
More...
#include <Neighbours_Rn.h>

Public Member Functions | |
| Neighbours_Rn () | |
| void | addGenerator (const std::vector< unsigned int > &commonFacets, unsigned int numbergenIN, unsigned int numbergenOUT, HalfSpace_Rn::State state) |
| Tell whether a pseudo neighbor is a genuine one comparing set of half-spaces. More... | |
| void | addGeneratorWithoutCheck (const std::vector< unsigned int > &commonFacets, unsigned int numbergenIN, unsigned int numbergenOUT, HalfSpace_Rn::State state) |
| void | begin () |
| Iterator function. More... | |
| void | next () |
| Iterator function. More... | |
| void | checkIterator () |
| Make sure we don't point on a generator with state ON. More... | |
| bool | end () const |
| Iterator function. More... | |
| unsigned int | currentGenInNumber () const |
| Iterator function. More... | |
| unsigned int | currentGenOutNumber () const |
| Iterator function. More... | |
| const std::vector< unsigned int > & | commonHalfSpaces () const |
| Iterator function. More... | |
| void | dump (std::ostream &ofs) const |
| Display the content on the stream passed as an argument. More... | |
Protected Attributes | |
| unsigned int | _iterator |
| A runner to iterate through the list of genuine neighbors. More... | |
| std::vector< HalfSpace_Rn::State > | _GeneratorsState |
| The pair of generators state. More... | |
| std::vector< unsigned int > | _GeneratorsInNumber |
| The generator numbers IN in a global list. More... | |
| std::vector< unsigned int > | _GeneratorsOutNumber |
| The generator numbers OUT in a global list. More... | |
| std::vector< std::vector< unsigned int > > | _HSPerNewGenerators |
| For each generator, store all raw pointers on their corresponding half-spaces. More... | |
Detailed Description
Class dedicated to degeneration processing when looking for neighbours.
Let A be a polytope of \( \mathbb{R}^n, A = H_1^+ \cap H_2^+ \cap ... H_{n-1}^+ \cap ... H_k^+ \) where k>n.
Let [vi, vj] be a segment of two vertices of A such as:
- they share (n-1) hyperplanes in common: \( H_{ij} = \{ H_1, H_2, ... H_{n-1} \} \)
- there exists an hyperplane \( \mathcal{H} \) separating [vj, vk]
We call [vi, vj] a pseudo-edge if it respects the first assumption. The question is: to which condition [vi, vj] is a genuine edge? Can we answer the question only by processing the pseudo-edges separated by the hyperplane \( \mathcal{H} \)? The straight line \( (v_i, v_j) \subset H_1 \cap H_2 \cap ... H_{n-1} \text{~with~} \mathcal{H} \neq H_u \), \( u \in \{ 1, ..., n-1 \} \). So \( H_1 \cap H_2 \cap ... H_{n-1} \cap H_n^+ \cap ... H_k^+ = F_A \) is a face of A of dimension at least 1. Let's assume [vi, vj] is not an edge of A, then it is not an edge of FA and we cannot have FA included neither in \( \mathcal{H}^+ \) nor in \( \mathcal{H}^- \) as \( \mathcal{H} \) separates [vi, vj] . So \( \mathcal{H} \) separates FA and we can find an edge [va, vb] of FA such as:
- \( \mathcal{H} \) separates [va, vb] or
- \( \mathcal{H} \) passes through va or
- \( \mathcal{H} \) passes through vb
As [va, vb] is an edge of FA, va and vb share in common the list of hyperplanes Hab . Hab contains the (n-1) half-spaces \( H_1, H_2, ... H_{n-1} \) and others because the intersection \( H_1 \cap H_2 \cap ... H_{n-1} \) does not define a straight line. So if [vi, vj] is not an edge of A, we can find a genuine edge [va, vb] , intersecting with \( \mathcal{H} \), such as \( H_{ij} \subset H_{ab} \)
Definition at line 59 of file Neighbours_Rn.h.
Constructor & Destructor Documentation
◆ Neighbours_Rn()
|
inline |
Definition at line 62 of file Neighbours_Rn.h.
Member Function Documentation
◆ addGenerator()
|
inline |
Tell whether a pseudo neighbor is a genuine one comparing set of half-spaces.
- Parameters
-
commonFacets the set of common half-spaces pointers between this and gen numbergenIN the generator number candidate to be a genuine end of edge numbergenOUT the generator number candidate to be the other genuine end of edge state equal to HalfSpace_Rn::hs_IN_OR_OUT or HalfSpace_Rn::hs_ON according to the edge property
Definition at line 69 of file Neighbours_Rn.h.

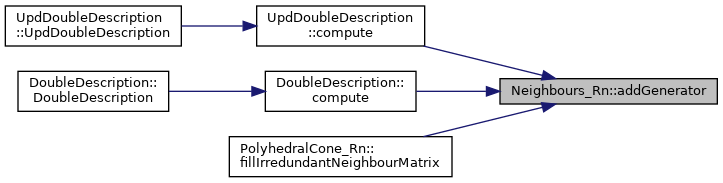
◆ addGeneratorWithoutCheck()
|
inline |
Definition at line 127 of file Neighbours_Rn.h.
◆ begin()
|
inline |
Iterator function.
Definition at line 139 of file Neighbours_Rn.h.

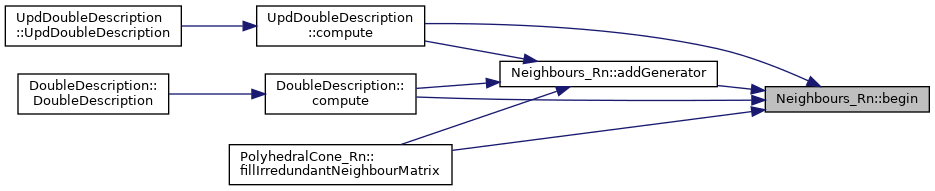
◆ checkIterator()
|
inline |
Make sure we don't point on a generator with state ON.
Definition at line 145 of file Neighbours_Rn.h.

◆ commonHalfSpaces()
|
inline |
Iterator function.
Definition at line 160 of file Neighbours_Rn.h.

◆ currentGenInNumber()
|
inline |
Iterator function.
Definition at line 154 of file Neighbours_Rn.h.
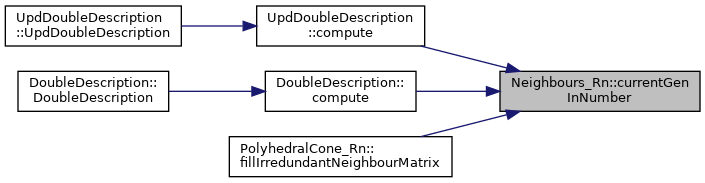
◆ currentGenOutNumber()
|
inline |
Iterator function.
Definition at line 157 of file Neighbours_Rn.h.
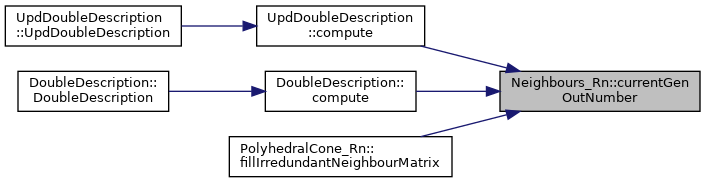
◆ dump()
|
inline |
Display the content on the stream passed as an argument.
Definition at line 163 of file Neighbours_Rn.h.


◆ end()
|
inline |
Iterator function.
Definition at line 151 of file Neighbours_Rn.h.
◆ next()
|
inline |
Iterator function.
Definition at line 142 of file Neighbours_Rn.h.

Member Data Documentation
◆ _GeneratorsInNumber
|
protected |
The generator numbers IN in a global list.
Definition at line 183 of file Neighbours_Rn.h.
◆ _GeneratorsOutNumber
|
protected |
The generator numbers OUT in a global list.
Definition at line 185 of file Neighbours_Rn.h.
◆ _GeneratorsState
|
protected |
The pair of generators state.
Definition at line 181 of file Neighbours_Rn.h.
◆ _HSPerNewGenerators
|
protected |
For each generator, store all raw pointers on their corresponding half-spaces.
Definition at line 187 of file Neighbours_Rn.h.
◆ _iterator
|
protected |
A runner to iterate through the list of genuine neighbors.
Definition at line 179 of file Neighbours_Rn.h.
The documentation for this class was generated from the following file:
- /mnt/c/Users/vindelos/Documents/TEST/TEST/co/politopix/trunk/Neighbours_Rn.h
