This inheritance list is sorted roughly, but not completely, alphabetically:

[detail level 1234]

CconstIteratorOfListOfGeometricObjects< GEOMETRIC_OBJECT >	This class is designed to run the list of all geometric objects representing a polytope
CDoubleDescription< POLYHEDRON, ITERATOR, REDUNDANCY_PROCESSING >	The algorithm implemented here is an incremental algorithm as mentioned in How Good are Convex Hull Algorithms? (1997) by David Avis and David Bremner. Specific and efficient implementations can be found in The double description method revisited (1996) written by Komei Fukuda and Alain Prodon . Incremental algorithms for the vertex enumeration problem compute the vertex description by intersecting the defining half-spaces sequentially. An initial simplex is constructed from a subset of n+1 half-spaces and its vertices and 1-skeleton are computed. Additional half-spaces are introduced sequentially and the vertex description and 1-skeleton are updated at each stage. Essentially such an update amounts to identifying and removing all vertices that are not contained in the new half-space, introducing new vertices for all intersections between edges and the bounding hyperplane of the new half-space, and generating the new edges between these new vertices. This algorithm can be instantiated by polytopes or polyhedral cones, and as a second argument can be instantiated by iterators such as minindex, lexmin, lexmax
CDoubleDescriptionFromGenerators	Compute the V-description from the H-description
CFaceEnumeration	Combinatorial face enumeration for polytopes
CGenerator_Rn	A n-coordinates generator, which can be a vertex or an edge whether it is contained by a polytope or a polyhedral cone. It contains all of its support facets
CGenerator_Rn_SD	A n-coordinates generator for internal data structure. It can be a vertex or an edge whether it is embedded in a polytope or a polyhedral cone. It contains all of its support facets
CHalfSpace_Rn	A half-space whose frontier is a linear (n-1) dimension space. _constant + _coefficients[0].x1 + ... + _coefficients[n-1].xn >= 0
CIO_Polytope	Read/write polytopes. The way we store polytopes : 1st line : comments = "# Dimension NumberOfHalfspaces NumberOfGenerators" 2nd line : cartesian_space_dimension number_of_facets number_of_generators 3rd line : comments = "# HALFSPACES : a0 + a1.x1 + ... + an.xn >= 0." 4th line : a00 a10 ... an0 k-th line : a0k a1k ... ank (k+1)-th line : comments = "# GENERATORS : V = (v1, ..., vn)" (k+2)-th line : v11 ... v1n l-th line : vl1 ... vln (l+1)-th line : comments = "# FACETS PER GENERATOR : {Fi1, Fi2, ...}" (l+2)-th line the neigh : Fr ... Fs m-th line : Fs ... Ft If (number_of_vertices == 0) then compute the vertices from the facets including the polytope into a huge cube containing it. In this case the blocks "GENERATORS" and "FACETS PER GENERATOR" are ignored
▼ClexIteratorOfListOfGeometricObjects< GEOMETRIC_OBJECT >	Insert the half-spaces in the list in a lexicographically order, whether min or max
ClexmaxIteratorOfListOfGeometricObjects< GEOMETRIC_OBJECT >	Insert the half-spaces in the list in lexicographically decreasing order
ClexminIteratorOfListOfGeometricObjects< GEOMETRIC_OBJECT >	Insert the half-spaces in the list in lexicographically increasing order
ClistOfGeometricObjects< GEOMETRIC_OBJECT >	This class is designed to contain the list of all generators or half-spaces representing a polytope or a polyhedral cone
ClistOfGeometricObjects< boost::shared_ptr< Generator_Rn > >
ClistOfGeometricObjects< boost::shared_ptr< HalfSpace_Rn > >
▼CMinkowskiSum	Compute the Minkowski sum of two polytopes
CPseudoSumWithoutCaps	Compute the Minkowski sum of two polytopes and then remove all cap half-spaces to truncate again
CNeighbours_Rn	Class dedicated to degeneration processing when looking for neighbours. Let A be a polytope of 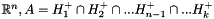$\mathbb{R}^n, A = H_1^+ \cap H_2^+ \cap ... H_{n-1}^+ \cap ... H_k^+$ where k>n. Let [v_i, v_j] be a segment of two vertices of A such as:
CNoRedundancyProcessing< POLYHEDRON >	Makes the assumption we do not need to process redundant half-spaces in a specific way
CNormalFan_Rn	Model a normal fan
CPoint_Rn	Creation of a n-coordinate geometric point designed to be shared by its neighbour faces
CpolitopixAPI	The main class to run the basic API
▼CPolyhedralCone_Rn	Model a polyhedral cone using its two equivalent definitions : the convex hull and the half-space intersection. We store its edges in _listOfHS and the positive combination of these vectors generates the polyhedral cone
CPolytope_Rn	Model a polytope using its two equivalent definitions : the convex hull and the half-space intersection
CPolytopeToSimplexes
CPseudoIntersectionWithoutCaps	Remove all cap half-spaces and then compute the intersection of two capped polytopes
CRealNeighbours	Class dedicated to degeneration processing when looking for neighbors
CRn	This class stores static function that dispatch the main geometric values we use
CsortOnFirstCoord
CStrongRedundancyProcessing< POLYHEDRON >	This class can be more time-consuming than WeakRedundancyProcessing or NoRedundancyProcessing because it will perform extra checks in the process of intersecting half-spaces. To determine if two vertices are neighbors it will make sure not to count half-spaces marked as redundant
CTopGeomTools	Basic tools for topology and geometry: translations, polarity, ..
CTrackingBinaryOperation	This class stores static function that dispatch the main geometric values we use
CTrackingOperatorToResult	This class stores static function that dispatch the main geometric values we use
CVisualization	2D visualization tools
CVolumeOfPolytopes_Rn	Split a polytope into simplices to compute its volume. Two Algorithms for Determining Volumes of Convex Polyhedra (1979) by Jacques Cohen and Timothy Hickey Journal of the ACM (JACM) JACM Homepage archive Volume 26 Issue 3, july 1979 Pages 401-414
▼CVoronoi_Rn	Compute a n-dimensional Voronoi diagram. It is a partitioning of a space into regions based on distance to points. Both the space and the list of points are provided as input
▼CCellByCellVoronoi	Computes the Voronoi diagram cell by cell
▼CCellByCellVoronoiDist	Constructor
CCellByCellVoronoiDistNgb	Do the same as CellByCellVoronoiDist with the neighbourhood computation
CIncrementalVoronoi	At the end of the ith iteration, the Voronoi diagram of i seeds is computed
CVoronoiWithProperties	Fuse Voronoi cells when they share the same property and then get non convex polytopes